縦、横、高さ+時間の4次元空間のこと。 つまり、時間と空間。
時間と空間を合わせた物理学の用語です。相対性理論では、時間と空間は独立ではなく、四次元空間として扱われます。
時空についてわかりやすく説明すると、次のようなことが挙げられます。
- 時空は、時間と空間の統一体です。
- 時空は、物質の質量によって歪みが生じ、その歪みが重力となります。
- 時空は、相対性理論によって、時間と空間が伸び縮みするものとして考えられています。
- 時空は、相対性理論によって、時間と空間が互いに関連したものとして考えられています。
時空に関する具体的な例としては、次のようなものがあります。
- 高速で移動するロケットの中では空間が縮み、時間の進み方が遅れます。
- 巨大な重力をもつ天体の近傍では光の経路が曲がる重力レンズとして観測されます。
- 重力の違いによって時間の進み方が異なります。
- この歪みが光速度の波として伝わるものを重力波といいます
空間は当然のものと考えられてきた。空間とはつまりは空っぽであり,その他すべての背景だ。時間も同様に,単に絶え間なく経過していく。だが物理学者が数々の理論の統合を目指すその長い苦闘から学んだものがあるとすれば,それは空間と時間が驚異的に複雑な1つの系を形成していて,その理解を試みるいかなる努力も寄せつけないかもしれないということだ。
アインシュタイン(Albert Einstein)は1916年11月に,早くもそれに気づいていた。一般相対性理論をまとめる1年前だ。一般相対論は重力を,空間を伝わる力ではなく,時空そのものが持つ性質であると考える。空高く投げ上げたボールが弧を描いて地面に戻ってくるのは,地球が周囲の時空をゆがめているためで,それによってボールの軌跡が地面と再び交わるからだ。アインシュタインは友人に宛てた手紙のなかで,一般相対論と,彼の別の考案である草創期の量子力学理論を融合することの困難を嘆いた。両者を統合しようとすると空間が単にゆがむだけではすまず,解体してしまう。数学的にどこから手をつければよいのか,まるで見当がつかなかった。「自分自身の考案にこんな形でこうも苦しめられるとは!」と書いている。
この問題について,アインシュタインはたいした前進なしに終わった。量子重力理論に関しては現在も数多くのアイデアが競合している。このテーマを研究する科学者の人数とほぼ同数の理論があるといえる。そうした論議に目を奪われると,ある重要な事実を見落とす。それら競合するアプローチのすべてが,空間はもっと根本的な何かから生じると述べていることだ。
一般相対性理論とは?
アインシュタインが構築した一般相対性理論は、慣性系だけでなく、加速度運動している(外力が働いている)座標系における運動に対しても適用できる理論です。慣性系という足かせが取れたので、ここで“一般”という名前がつくようになりました。
アインシュタインは、このとき簡単な仮定を採用しました。それは等価原理と呼ばれるもので、
“運動における加速度”と”重力による加速度”は区別できない
というものです。ただし、この原理は局所的に(非常に狭い領域で)見たときに成立するものです。アインシュタインがこの等価原理に気づいたのは、特殊相対性理論の発表からわずか2年後、1907年のことでした。彼自身「生涯で最も素晴らしいアイデア」と自画自賛したアイデアです。
一般相対性理論には、等価原理の他に、もう一つの重要な要素が出てきます。それは”曲がった時空”です。なぜなら、一般相対性理論における重力の効果は時空の曲がりとして出てくるからです。
曲がった時空とは?
一般相対性理論では、”時空の曲がり”も一つの大切なキーワードです。
私たちは日常生活の中で、時空が曲がっていることを認識することはありません。もし、あったら大変です。まっすぐ歩くことはできなくなるからです。重力はそもそも非常に弱い力であり、身の回りに膨大な質量を持つ物体もありません。身近にあるとすれば、それは地球であり、太陽ぐらいのものです。
曲がっていない時空はユークリッド空間と呼ばれ、そこで成立する幾何学はユークリッド幾何学と呼ばれます。ユークリッド空間では平行線はいつまでも平行線であり、また三角形の内角の和は180度です。学校で習った通りです。つまり、私たちの日常感じている世界がユークリッド空間なのです。
時空が曲がっていない場合、光は直進します。これは光が伝播する場合、常に最短時間で伝播するためです。これはフランスの数学者、ピエール・ド・フェルマー(1608-1665)が1661年に発表したので、フェルマーの原理と呼ばれます。
しかし、一般相対性理論では、
・質量を持つ物体がある=その場所の時空は質量分布に応じて歪む
と考えるのです。
例えば、地球は太陽の周りを公転運動しています。ニュートン力学では地球と太陽の間に働く重力(地球は太陽の重力で引っ張られている)によると解釈します。しかし、一般相対性理論ではまったく異なる解釈になります。太陽の周辺は太陽の質量により時空が歪んでいます。地球はその歪んだ時空に沿って運動しているだけなのです。一般相対性理論はニュートン力学とはまったく異なる理論であることがわかると思います。
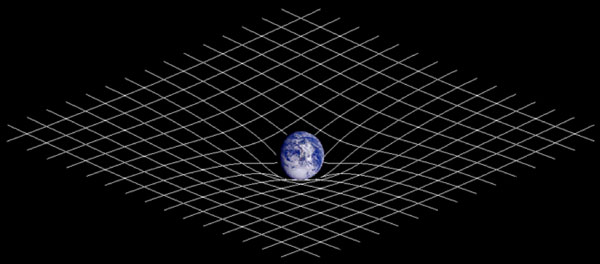
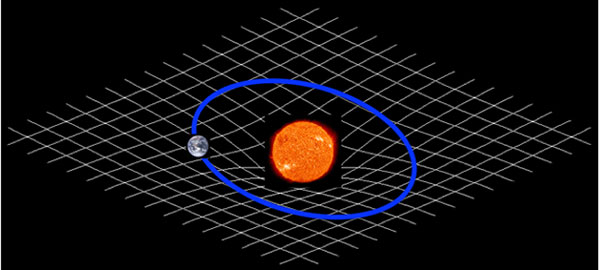
私たちが住んでいる世界はユークリッド空間であると言いました。曲がった時空はユークリッド空間ではないので、非ユークリッド空間と呼ばれます。非ユークリッド空間は厄介で、アインシュタイン自身を苦しめました。なぜなら、数学的な記述が格段と難しくなるからです。
だが、アインシュタインは幸運でした。彼には大学時代に数学に長けた友人がいたからです。友人の名前はマルセル・グロスマン(1878-1936)。ハンガリー出身の数学者です。チューリッヒ工科大学の数学科の教授だったグロスマンは、アインシュタインに非常に有益なコメントを与えました。
「君の理論に必要なのはリーマン幾何学だよ」
リーマン幾何学は非ユークリッド空間を取り扱える幾何学で、微分幾何学と呼ばれる幾何学の一種です。ドイツの数学者ベルンハルト・リーマン(1826-1866)によって創設された幾何学体系です。曲がった時空を取り扱うことになるので、なにしろ難解になります。
下の図を見てください。
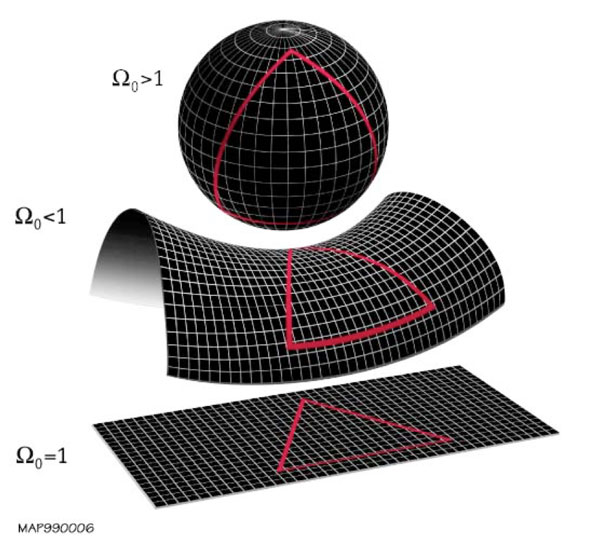
上から、閉じた宇宙、開いた宇宙、そして平坦な宇宙(ユークリッド空間)です。三角形の内角の和は、閉じた宇宙では180度より大きくなり、開いた宇宙では小さくなります。平行線も、閉じた宇宙では交わってしまいますが、開いた宇宙では交わることもあれば、交わらずに離れていく場合もあります。平坦な宇宙とは明らかに異なった状況になっていることがわかると思います。
質量を持つ物体があると、その周りの時空が曲がり、それが重力の効果として現れる。一般相対性理論ではこのように重力を考えるので、曲がった時空を記述するリーマン幾何学が必須になるのです。
例えば、ある距離を置いて、地球の赤道上の二つの地域から飛行機を飛ばすとしましょう。2機の飛行機はいずれも真北に向かって飛んでいきます。高度も1万メートルを保って飛ぶとしましょう。お互いの飛行機から眺めると、しばらくは2機は平行に飛んでいるように見えます。しかし、厳密に眺めると、2機は少しずつ近づいているのです。そして、北極点に達したとき、悲劇が起こります。2機はあえなく衝突してしまうからです。
出発地点ではお互いにきちんと真北に向かいました。つまり、平行に飛び始めた。ところが、飛行機は真に平行に飛ぶわけではないのです。地球というほぼ球体の表面の上を飛ぶからです。つまり、2機の航路は直線ではなく、空間を曲がりながら飛んだのです。これは曲がった空間を飛んだことに等しくなります。そのため、平行からずれて北極点で衝突してしまったのです。
また、少し離れたところにいる2人の人間が、地球の中心に向かって落ち込んでいくときも同じような出来事が起こります。最初、2人は離れており、地球の中心に向かって平行を保ちながら落ちていくように感じられるでしょう。しかし、中心に近づくにつれて2人の距離は少しずつ近づいていきます。そして中心では、2人は見事に衝突してしまいます。彼らも、じつは曲がった空間を移動していたのです。
※
以上、『宇宙はなぜブラックホールを造ったのか』(谷口義明著、光文社新書)から抜粋し、一部改変してお届けしました。